数据结构 —— 堆

Administrator

2021-08-11

数据结构堆

704

优先队列

讲 堆 之前，先讲一个堆的典型用处，就是 优先队列。优先队列 有两个操作，分别是入队和出队。和队列有一点像，但是并不是先进后出，而是优先度高的先出

对于优先队列，可以理解为内部会自动对队中的元素进行排序，永远保证对头的元素永远是优先度最高的，例如图中就是较小的数优先。

对于出队操作就和普通队列一样了

如果数量不大的数据，可以使用链表实现优先队列，只需要入队的时候为元素提供上浮操作就行，但这种操作的入队的最差时间复杂度为 o(n)，n 为 队中 元素个数，显然这个效率比较低，而如果用堆实现的话，在大量数据下可以显著提升效率。接下来来实现一个堆吧。

堆 - 逻辑结构

其实对于 堆，其逻辑结构就是 二叉树，并且是 完全二叉树，并且满足以下条件：

根节点的优先度大于其左右孩子。
根的左右子树也满足 堆 的条件

这里的优先度其实是可以自定义的规则，只要能比较两个数据即可，可以是数字大小等。

对于优先度规则为数字大小的，如果是较小的数优先度大，则称为 小顶堆，反之则为 大顶堆。

首先让我们画一个已经满足条件的 小顶堆（注意 堆 必须是完全二叉树）

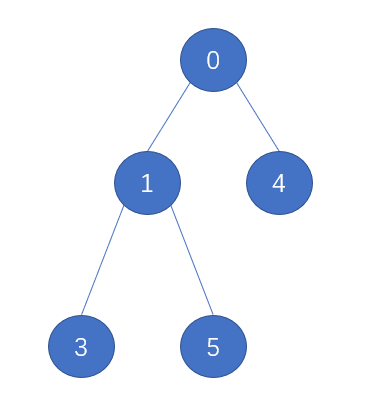
现在我们在最后的位置加入一个节点 2

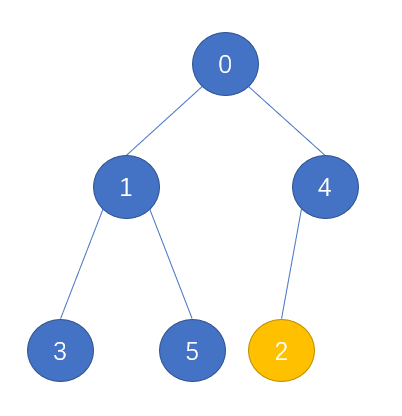
可以看到这里加入了新节点之后，堆不满足要求了，现在我们可以对新加入的节点进行 上浮 操作：

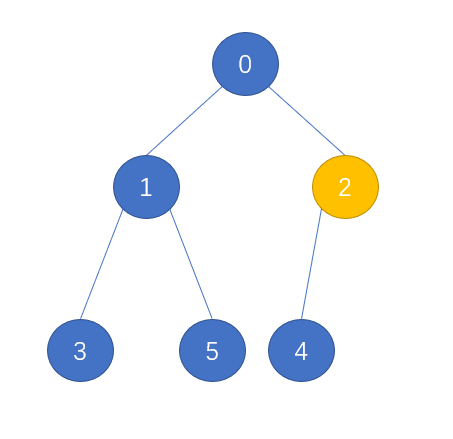
上浮

也正如刚才看到的效果，上浮操作其实是一个递归的过程，不断比较节点与双亲的优先度，如果节点优先度比双亲还大，则交换，知道没有双亲或满足堆的要求。

实际上，对于上浮操作，是有要求的：

堆去掉要上浮的节点及其所有后代后满足堆的要求

只有满足以上要求，在做完上浮操作后，才会满足堆的要求。

下沉

与 上浮 类似，下沉 操作也是一个递归的过程，不断地比较节点与其左右孩子的优先度，如果节点的优先度最大，则不作任何处理，否则将节点与孩子中优先度最大的节点交换。

下沉操作也有条件：

节点的左右子树要满足堆的要求

堆的操作

首先对于堆有以下操作：

入堆
出堆
取堆顶
判堆空

取堆顶 就是直接取根节点的元素，判堆空 则是直接判定节点个数，这两个操作比较简单。这里主要看 入堆 和 出堆 操作：

对于 入堆 操作，是直接在堆中加入节点，因为 堆 一定是 完全二叉树 ，所以加入节点的位置是确定的，并且刚加入的节点一定是叶子结点。所以对于这个节点其肯定满足 上浮 的条件，因此可以直接对加入的节点进行 上浮 操作。

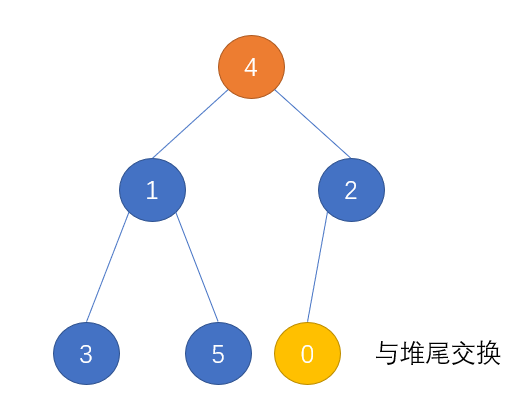
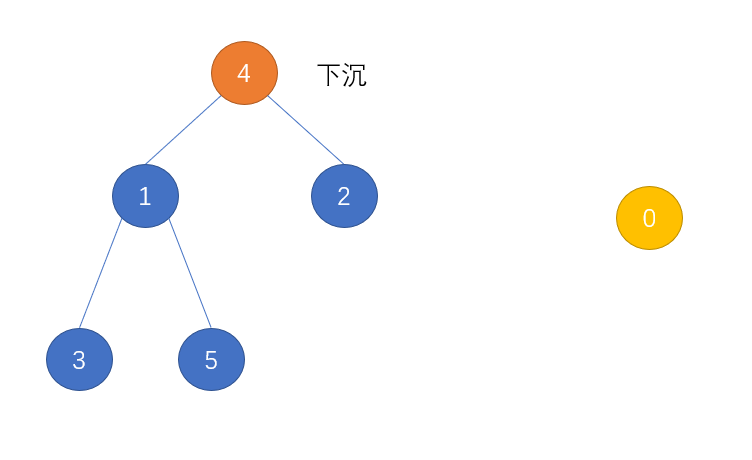
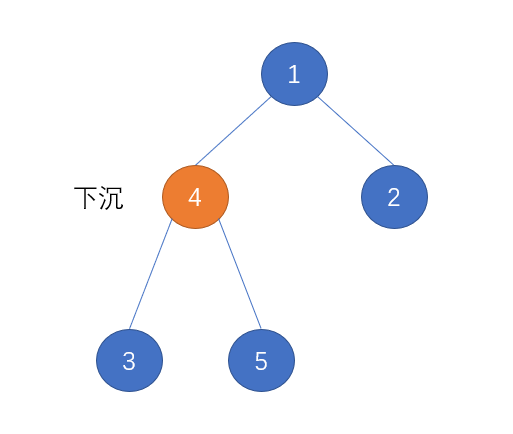
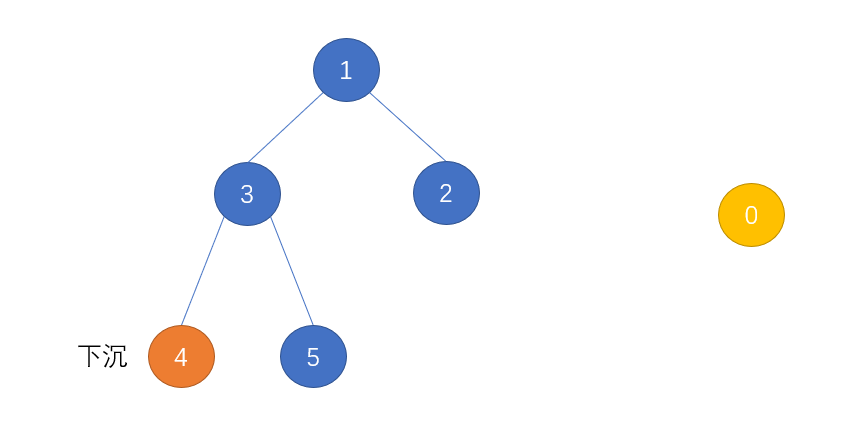
对于 出堆 操作，是要删除其根节点，这里的操作就比较麻烦，我们是将根节点与堆尾节点交换，然后删除堆尾节点，此时根节点满足下沉条件，可以对根节点进行下沉操作：

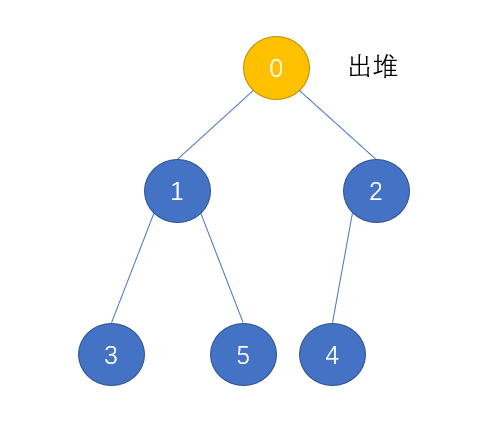
堆的物理结构

虽然说 堆 的逻辑结构是 完全二叉树，但是其物理结构并不是二叉树，因为 完全二叉树 是一种很特殊的二叉树，我们可以对其节点进行标号：（节点中数字只是标号，并不作为实际数据）

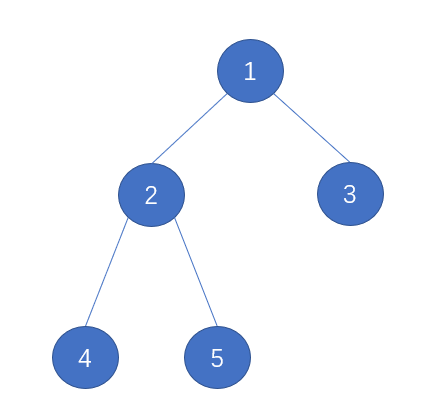
我们发现对于标号为 i 的节点，其双亲节点的标号为 ⌊i/2⌋（下取整），其左孩子的标号为 2*i 其右孩子的标号为 2*i+1。

因此我们可以使用数组来存储二叉树的结构，并通过 下标 来对应节点的 标号 建立一一对应的关系。因为数组的下标是从 0 开始，因此节点的 标号 为 下标 +1

堆的代码实现

这里使用 C 语言来实现：

头文件：

#ifndef HEAP_HEAP_H
#define HEAP_HEAP_H

#define INIT_CAPACITY 32
#define NULL ((void*)0)

#include <stdlib.h>

typedef struct Heap{
    int *data;
    int size;
    int capacity;
} Heap;

int Heap_InitByArray(Heap *h, int* data, int size);
int Heap_Init(Heap *h);
void Heap_ShiftUp(Heap *h, int i);
void Heap_ShiftDown(Heap *h, int i);

int Heap_Push(Heap *h, int elem);
int Heap_Top(Heap* h, int *top);
int Heap_Pop(Heap* h);

int Heap_Empty(Heap* h);

void Heap_Free(Heap*h);
#endif //HEAP_HEAP_H

然后是各个方法：

根据数组初始化

int Heap_InitByArray(Heap *h, int* data, int size){
    if(h == NULL){
        return 0;
    }
    int ss = size/INIT_CAPACITY +1;
    h->capacity = ss*INIT_CAPACITY;
    h->size = 0;
    for(int i = 0 ; i < size ; i ++){
        h->data[h->size] = data[i];
        Heap_ShiftUp(h, h->size +1);
        h->size ++;
    }
    return 1;
}

初始化空堆

int Heap_Init(Heap *h){
    if(h == NULL){
        return 0;
    }
    h->capacity = INIT_CAPACITY;
    h->data = (int*) malloc(INIT_CAPACITY * sizeof(int));
    h->size = 0;
    return 1;
}

上浮

void Heap_ShiftUp(Heap *h, int i){
    if(h == NULL){
        return;
    }
    while(i /2 >= 1){
        if(h->data[i/2-1] > h->data[i-1]){
            int c = h->data[i/2-1];
            h->data[i/2-1] = h->data[i-1];
            h->data[i-1] = c;
            i/=2;
        }else{
            break;
        }
    }
}

下沉

void Heap_ShiftDown(Heap *h, int i){
    if(h == NULL){
        return;
    }
    while(i*2 <= h->size){

        int left = i*2;
        int right = i*2+1;
        if(right <= h->size && h->data[left-1] > h->data[right-1]){
            left = right;
        }

        if(h->data[left-1] < h->data[i-1] ){
            int c = h->data[left-1];
            h->data[left-1] = h->data[i-1];
            h->data[i-1] = c;
            i = left;
        }else{
            break;
        }

    }
}

入堆

int Heap_Push(Heap *h, int elem){
    if(h == NULL){
        return 0;
    }
    if(h->size == h->capacity){
        // 扩容
        int ca = h->capacity + INIT_CAPACITY;
        int* data = (int*) malloc(ca*sizeof(int));
        if(data == NULL){
            return 0;
        }
        for(int i = 0 ; i < h->size ; i ++){
            data[i] = h->data[i];
        }
        free(h->data);
        h->data = data;
        h->capacity = ca;
    }

    h->data[h->size] = elem;
    Heap_ShiftUp(h, h->size+1);
    h->size ++;
    return 1;
}

取堆顶

int Heap_Top(Heap* h, int* top){
    if(h == NULL){
        return 0;
    }
    if(h->size == 0){
        return 0;
    }
    *top = h->data[0];
    return 1;
}

出堆

int Heap_Pop(Heap* h){
    if(h == NULL){
        return 0;
    }
    if(Heap_Empty(h)){
        return 0;
    }
    int c = h->data[h->size -1];
    h->data[h->size-1] = h->data[0];
    h->data[0] = c;
    h->size --;
    Heap_ShiftDown(h, 1);
    return 1;

}

判堆空

int Heap_Empty(Heap* h){
    if(h == NULL){
        return 0;
    }
    return h->size==0;
}

释放堆内存

void Heap_Free(Heap*h){
    free(h->data);
    free(h);
}